cours de physique                                                                       SATELLITES  ET  PLANETES

 

Le mouvement des planètes est étudié dans le référentiel héliocentrique. Il obéit aux lois de Kepler.

1 LES LOIS DE KEPLER

1-1. Historique :

Dès l'Antiquité, les astronomes ont essayé de prévoir les déplacements des planètes.

Pour Ptolémée (Ile siècle ap. J .-C.), qui élabore un modèle complexe, la Terre, autour de laquelle tournent le Soleil et les planètes, occupe le centre du monde.

En 1543, Copernic (1473-1543) publie un traité, De Revolutionibus, selon lequel le Soleil est le centre du Monde.

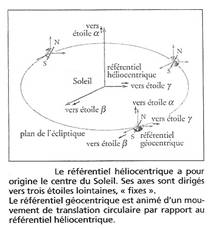
Copernic est à l'origine du système héliocentrique. Dans le référentiel héliocentrique (du grec hêlios, « soleil )} ) , les neuf planètes du système solaire ont des trajectoires quasi circulaires centrées sur le Soleil.

Utilisant les résultats des observations de son maître Tycho Brahé (1546-1601), Kepler (1571-1630) formule les trois lois qui décrivent le mouvement des planètes autour du Soleil.

 

1-2. Les trois lois de Kepler

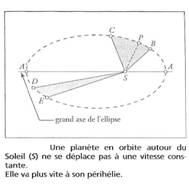
PREMIÈRE LOI : loi des trajectoires

Dans le référentiel héliocentrique, le centre d’inertie d'une planète décrit une ellipse dont le Soleil occupe l’un des foyers.

Ellipse : voir fig 4 p 252 et TP

Le cercle est une ellipse particulière dont les deux foyers sont confondus avec le centre.

DEUXIÈME LOI: loi des aires

Les aires balayées, pendant des durées égales, par le segment de droite reliant le centre d’une planète à celui du Soleil, sont égales.

TROISIÈME LOI: loi des périodes

Le rapport du carré de la période de révolution T d’une planète au cube du demi-grand axe a de l’ellipse est constant.

 

 = k = constante

 

Cette constante k est la même pour toutes les planètes du système solaire, elle dépend de la masse du Soleil.

Remarques :

·         Dans le cas des satellites dont la trajectoire est assimilable à un cercle de rayon r, la troisième loi de Kepler s’écrit :  = k

2 MOUVEMENT CIRCULAIRE UNIFORME        

 

         On peut admettre que les planètes sont animées d'un mouvement circulaire uniforme ( à l’exception de Mercure et Pluton, les ellipses décrites par les autres planètes ont une très faible excentricité )

2-1. Définition :

Un mobile a un mouvement circulaire uniforme si sa trajectoire est un cercle et si la valeur v de sa vitesse est constante.

Etude fig 7 p 253 : on choisit un point origine et un sens positif de rotation, on peut repérer la position du point M par la valeur de l’angle θ en radian

La vitesse angulaire en rad.s-1 est telle que v = r w où ( r : rayon du cercle décrit )

Dans un mouvement circulaire uniforme, la vitesse angulaire est constante.

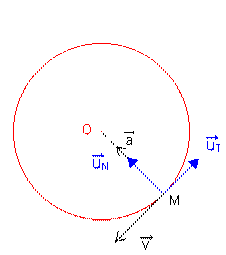
2-2. Vecteur vitesse

      

direction : tangente à la trajectoire

sens : celui du mouvement

valeur v= constante

Le vecteur vitesse a une valeur v constante mais il change de direction, il n’est pas constant

En prenant un vecteur unitaire  porté par la tangente à la trajectoire et orienté dans le sens positif, on peut écrire à chaque instant :

=  vt   = +/- v

2-3. Vecteur accélération

(voir activité du TP)

Dans le cas d’un mouvement circulaire uniforme, le vecteur accélération est tel que

 

direction : normale à la trajectoire, dirigé suivant un rayon du cercle : le vecteur accélération est radial

sens : vers le centre du cercle, il est centripète.

valeur a =

 

En prenant un vecteur unitaire , radial et centripète, on peut écrire  =  

 et  constituent les vecteurs unitaires de la base de Frenet

Dans le cas d'un mouvement circulaire uniforme, v est une constante donc  = O  et l’accélération s’écnt :

 

 ( t ) =  .

 

L'accélération, dans le cas d’un M.C.U., est donc radiale centripète, de valeur

2-4. périodicité d’un mouvement circulaire uniforme

Le mobile repasse à intervalles de temps égaux dans la même position, en allant dans le même sens. Le mouvement est périodique.

 

La période de révolution T est égale à la durée d’un tour : 

T =  =

 

La période de révolution de la Terre autour du Soleil est égale à 365,25j

2-5.Conditions nécessaires pour observer un mouvement circulaire uniforme :

La deuxième loi de Newton appliquée à un système de masse m et de centre d’inertie G donne

                           =    =  m .  = m .  = m .

 

en conséquence, les conditions nécessaires pour observer un mouvement circulaire uniforme sont :

 

Ä         une vitesse initiale v non nulle

Ä         une résultante  des forces radiale, c'est-à-dire dirigée vers un point fixe O

 

 

Dans ces conditions,

Ä         O est le centre de la trajectoire circulaire

Ä         la valeur F de la résultante des forces et la vitesse v du système en mouvement circulaire uniforme sont liées par la relation :   =   m .

3 MOUVEMENT DES SATELLITES ET DES PLANETES

3-1.Loi de la gravitation de Newton :

Ä                  Loi de la gravitation entre 2 corps ponctuels A et B

Notion rencontrée en seconde : l'interaction gravitationnelle             

est une interaction fondamentale dont la portée est infinie.

Elle a été exprimée pour la première fois par Isaac Newton (1687).

Loi de Newton :

Deux objets ponctuels (A) et (B) de masse mA et mB exercent l’un sur l’autre des forces attractives  et , de même direction, de sens opposé, et de même valeur.

mA et mB en kilogrammes  ( kg )

r en mètre  ( m )

FA/B en newton  ( N )

 

 

G est la constante de gravitation universelle.      G = 6,67 . 10-11 m3 . kg-1 . s-2      
                                                                              ( on écrit souvent G = 6,67 . 10-11 u.S.I. )

Ä                  expression vectorielle de la loi de Newton

On introduit un vecteur unitaire

 

 

    = - G   

 

et

 

 = -

Ä                  cas d’objets non ponctuels de centres respectifs A et B

Si les corps en interaction gravitationnelle ne sont pas ponctuels, les relations précédentes restent utilisables

--- si leur répartition de masse est à symétrie sphérique : la matière est répartie identiquement dans toutes les directions. ex : les planètes

---ou, si leur taille est faible devant la distance qui sépare les 2 corps en interaction  ex satellite par rapport à la terre Voir figure 10 p 254

 

3-1.Mouvement d’une planète autour du soleil

Ä                  référentiel héliocentrique

ce mouvement est étudié dans le référentiel héliocentrique( voir page 251)

Ä                  application de la deuxième loi de Newton

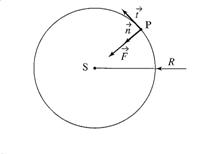On étudie une planète de centre d’inertie P, de masse m, en mouvement autour du Soleil de masse MS et de centre S. La distance SP sera notée r.

On peut assimiler la planète et le Soleil à des corps à symétrie sphérique.

bilan des forces : la force de gravitation exercée par le Soleil

                              = - G  = - G  

La deuxième loi de Newton s’écrit :

             

 

  =  = - G   = m         d’où     = - G = =

 étant un des 2 vecteurs de la base de Frenet définie plus haut.

est indépendant de la masse de la planète

radial : toujours dirigé selon la direction SP

centripète : pointe vers S

 

=  =

équation différentielle du mouvement

 

 

Ä                  solution de l’équation différentielle

On a vu que dans un mouvement circulaire uniforme,  =   

Le mouvement circulaire uniforme peut être solution de l’équation différentielle si  soit

 

 

v =

La planète décrit alors un cercle centré sur le Soleil, à la vitesse constante v =

Sa période de révolution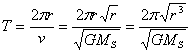

Le mouvement circulaire uniforme est uns solution particulière de l’équation différentielle.

C’est une approximation du mouvement des planètes d’autant plus satisfaisante que l’excentricité est faible

 

Ä                  troisième loi de Kepler

= k

            Comme vu dans l’activité k dépend de la masse de l’astre autour duquel tourne le satellite.

            k est une constante pour tous les satellites qui tournent autour du même astre.

            application numérique k =  pour les planètes du système solaire.

 

 

3.3.mouvement des satellites terrestres (prof)

 

Ce paragraphe est traité sous forme d’exercice. Les exemples choisis sont la Lune et le télescope Hubble. mais les résultats qui suivent peuvent s’adapter à n’importe quel satellite artificiel de la Terre.

a)La Lune

On admet que la Lune décrit une trajectoire circulaire, de rayon r = 384000 km, autour de la Terre

remarque :  r = RT + z où RT = rayon terrestre et z altitude du satellite par rapport à la terre.

La Terre est assimilée à une sphère de masse M = 6,0.10 24 kg et de rayon RT = 6400 km.

· 1 Définir le référentiel géocentrique.

le référentiel géocentrique est constitué par le centre O de la Terre et 3 directions allant du centre de la Terre à 3 étoiles considérées comme fixes.  Dans ce référentiel, la Terre a un mouvement de rotation propre de période égale à un jour sidéral : 86 400s voir fig 2 page 251

· 2 Faire le bilan des forces et utiliser la deuxième loi de Newton pour exprimer puis calculer dans le référentiel géocentrique la vitesse v de la lune et sa période de révolution T.

On utilisera les résultats de l’étude précédente (planètes autour du Soleil) qui peuvent être facilement transposés en remplaçant MS par MT

Constante de gravitation universelle : G = 6,67.10-11 S.I.

 

avec MCU solution de l’équation différentielle si

 

donc 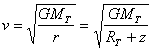 = =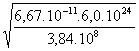1,02.103m.s-1

et =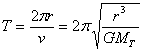

 

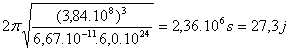
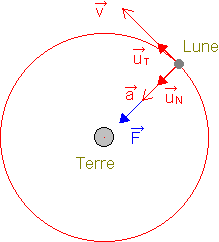
  3 pourquoi le Lune ne tombe-t-elle pas sur la Terre ?

La Lune subit de la part de la Terre une force qui l'attire vers celle-ci. A première vue, le problème ressemble à celui étudié pour le mouvement parabolique: la Lune possède une vitesse initiale et subit une force analogue au poids.

Alors, pourquoi la trajectoire de la Lune n'est-elle pas parabolique mais circulaire?

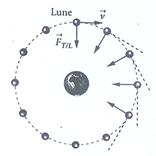La différence essentielle avec le mouvement parabolique tient au fait que la force de gravitation n'est pas uniforme: au cours du mouvement, la direction du vecteur force change. La Lune ne tombe pas sur la Terre mais tourne à vitesse constante dans le référentiel géocentrique parce que la force gravitationnelle exercée par la Terre est en permanence perpendiculaire à la direction de son mouvement.

b) vitesse et période d’un satellite terrestre

Vérifier que, pour les satellites terrestres, la vitesse et la période ne dépendent que de l’altitude z du satellite.

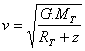 et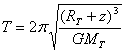

Quelle est l’influence de l’altitude sur la vitesse et la période d’un satellite terrestre ?

quand z augmente, la vitesse diminue et la période T augmente

c) la troisième loi de Képler

Etablir la troisième loi de Kepler pour un satellite terrestre et en déduire la période de révolution du télescope Hubble qui gravite autour de la Terre à l'altitude h = 600 km.

  donc 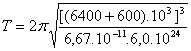= 5817s=1h37min

            d) les satellites géostationnaires

 

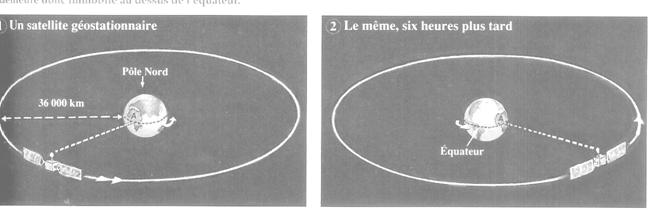
Ä     Définition

Un satellite est dit géostationnaire s'il reste en permanence à la verticale d'un point de la surface terrestre. Il occupe une position fixe dans le référentiel terrestre.

Quels sont les domaines d’utilisation des  satellites géostationnaires ?

télécommunications

Ä    

 

Conditions de stationnarité

Quelles conditions doit vérifier un satellite pour être géostationnaire?

.Lorsque la Terre tourne autour de l'axe des pôles, les satellites stationnaires tournent également avec elle. La trajectoire d'un satellite qui serait stationnaire au-dessus de Paris serait circulaire dans un plan qui ne passe pas par le centre de la Terre Cela est impossible. En effet, la trajectoire d'un satellite est dans un plan passant par le centre de la Terre. Ce n'est donc le cas que si le satellite est stationnaire au-dessus d'un point de l'équateur.

Un satellite ne peut être géostationnaire que si le plan de son orbite est confondu avec le plan de l'équateur (orbite équatoriale) Tout satellite géostationnaire se trouve à la verticale d'un point de l'équateur terrestre.

La période de révolution du satellite doit être la même que la période de rotation de la Terre autour de son axe polaire.

La période de révolution d'un satellite géostationnaire est égale à un jour sidéral. Sa valeur, notée Ts est égale à: Ts = 23 h 56 min 4 s = 86 ]64 s.

Le sens de rotation du satellite autour de la Terre et celui de la Terre autour de l'axe des pôles doivent être identiques.

Ces trois conditions étant réalisées, on peut désormais déterminer les caractéristiques cinématiques d'un satellite géostationnaire.

Ä      Détermination de l'altitude et de la vitesse d'un satellite géostationnaire Les conditions de stationnarité d'un satellite imposent la valeur de la période.

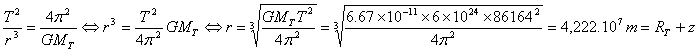
z = r-RT = 4,22.104 – 6400= 36000km

On en déduit sa vitesse :

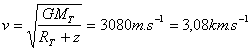
Un satellite géostationnaire évolue en orbite circulaire à une altitude proche de 36 000km et à une vitesse voisine de 3,1 km.s-1

            5) L’impesanteur

Imaginez-vous sur une table, une balle à la main et supposez qu’au moment où vous sautez de la table en lâchant la balle, le sol s’entrouvre sous votre immeuble et votre appartement ( qu’on peut assimiler à une boîte)s’y trouve précipité.

Que constate-t-on ?

Vous et la balle tombez dans une « boîte » qui ,elle-même, tombe. Or les 3 vitesses de chute sont identiques. En conséquence, ni vous, ni la balle ne rattraperez jamais le plancher qui semble vous fuir !

De même, si dans un satellite, un astronaute laisse échapper un objet, l’objet est immobile par rapport au satellite , il semble ne plus avoir de poids, on parle d’impesanteur.